Paper Summary #2: Convolutional Neural Network on Graphs with Fast Localized Spectral Filtering (NIPS 2016)

This post summarizes the NIPS 2016 paper by Defferrard et al on "Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering".

Convolutional Neural Networks have accomplished many breakthroughs, ranging from a classification of a million images of ImageNet to very complex tasks like object tracking in surveillance videos. These advancements are not restricted to image data. The CNNs (and, in general, deep learning concepts) have been able to achieve state-of-the-art results even on text and speech applications.

CNNs are proved to be very powerful tool in solving many problems from images, text and speech domain. If that is the case then the question that we want to ask here is, can we use CNNs to solve problems on graphs as well.

If we take a closer look at the data domain that we were dealing with, we realize that this data has specific structure, e.g. images are nothing but the 2-D grid of pixels, the text is a stream of words and can be thought of as a 1-D grid, as shown in figure 1 below. Such data, that has a regular structure, is said to be from the Euclidean domain.

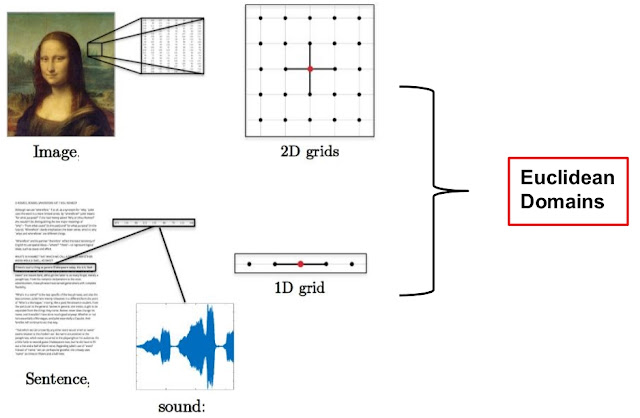Figure 1: Image data, text and speech data are Euclidean data as they have a regular structure. Convolution is well defined on this domain [source].

However, the data, on which we want to apply the CNNs, are the 3D shapes, brain functional network, protein network, social networks. etc. This type of data does not have any specific structure. Such data is said to be from the non-Euclidean domain. And this creates many challenges in applying CNNs on graphs.

Figure 2: These are the examples of non-Euclidean data. They have irregular structure and hence can't apply CNN directly in the spatial domain. [source]

The spatial convolution and pooling operations are well-defined only for the Euclidean domain. Hence, we cannot apply the convolution directly on the irregular structured data such as graphs.

To achieve our goal, we have to make use of Convolution Theorem which says 

Convolution in spatial domain is equivalent to multiplication in Fourier domain -Convolution Theorem.

As convolution in spatial domain is not defined for non-Euclidean data, we are going to make use of the convolution theorem. According to which, instead of performing convolution explicitly in the spatial domain, we will transform the graph data and the filter into Fourier domain. Do element-wise multiplication and the result is converted back to spatial domain by performing inverse Fourier transform. Figure 3 below shows this operation.

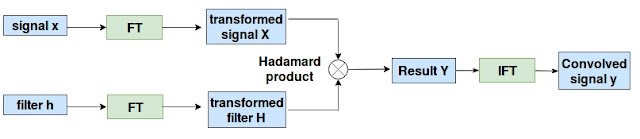Figure 3: The block diagram explaining the convolution theorem.

Now we know how to perform convolution on the non-Euclidean domain, the question remains, how to transform graph data into Fourier domain.

Graph Fourier Transform

In spectral graph theory, the important operator used for Fourier analysis of graph is the Laplacian operator. For the graph \(G=(V,E)\), with set of vertices \(V\) of size \(n\) and set of edges \(E\). The Laplacian is given by
\(\Delta = D - A\)
where \(D\) denotes the diagonal degree matrix and \(A\) denotes the adjacency matrix of the graph.

When we do eigen-decomposition of the Laplacian, we get the orthonormal eigenvectors, as the Laplacian is real symmetric positive semi-definite matrix (side note: positive semidefinite matrices have orthogonal eigenvectors and symmetric matrix has real eigenvalues). These eigenvectors are denoted by \(\{\phi_l\}_{l=0}^{n}\) and also called as Fourier modes. The corresponding eigenvalues \(\{\lambda_l\}_{l=0}^{n}\) acts as frequencies of the graph.

The Laplacian can be diagonalized by the Fourier basis.
\(\Delta=\Phi \Lambda \Phi^T\)
where, \(\Phi=\{\phi_l\}_{l=0}^{n}\) is a matrix with eigenvectors as columns and \(\Lambda\) is a diagonal matrix of eigenvalues \(\{\lambda_l\}_{l=0}^{n}\).

Now the graph can be transformed to Fourier domain just by multiplying by the Fourier basis. Hence, the Fourier transform of graph signal \(x:V \rightarrow \mathbb{R}\) which is defined on nodes of the graph \( x \in \mathbb{R}^n\) is given by:
\(\hat{x} = \Phi^T x\)
where \(\hat{x}\) denotes the graph Fourier transform. Hence, the task of transforming the graph signal to Fourier domain is nothing but the matrix-vector multiplication.

Similarly, the inverse graph Fourier transform is given by:
\(x = \Phi \hat{x}\).

Spectral Convolution Operation

As we now have the two necessary tools to define convolution on non-Euclidean domain: 1) way to transform graph to Fourier domain and 2) Convolution in Fourier domain, the convolution operation between graph signal \(f\) and filter \(g\) is given by:

\(f * g = \Phi g(\Lambda) \Phi^T f\)
where, \(g(\Lambda)\) is \(n\) x \(n\) matrix of spectral filter coefficient.

However, the above convolution operation has few limitations: (i) the filter is non-parametric i.e. the number of filter parameters to learn depends on the dimensionality of the input which means O(n) complexity. (ii) The filters are not localized i.e. filters learnt for graph considers the entire graph, unlike traditional CNN which takes only nearby local pixels to compute convolution. (iii) The algorithm needs to calculate the eigen-decomposition explicitly and multiply signal with Fourier basis as there is no Fast Fourier Transform algorithm defined for graphs, hence the computation is \(O(n^2)\). (Fast Fourier Transform defined for Euclidean data has \(O(nlogn)\) complexity)

These limitations can be overcome by approximating the spectral filter with polynomial of fixed order \(K\). In other words, we will use parametrized filter denoted by \(g_\Theta (\Lambda)\) where \(\Theta \in \mathbb{R}^K\) is vector of polynomial coefficients. In Graph Signal Processing, the traditionally used polynomial to approximate kernel is Chebyshev expansion, given by the recurrence relation: 
\(T_j(\lambda) = 2\lambda T_{j-1}(\lambda) - T_{j-2}(\lambda)\)
\(T_0(\lambda) = 1\)
\(T_1\lambda = \lambda\) 

The spectral filter is now given by a truncated Chebyshev polynomial:

\(g_\theta(\tilde{\Delta}) = \Phi g(\Lambda) \Phi^T\) 
             \(= \sum_{k=0}^{K} \theta_k  T_k(\tilde{\Lambda})\)

 where, \(\Theta \in \mathbb{R}^K\) now represents a vector of the Chebyshev coefficients, the \(\tilde{\Lambda}\) denotes the rescaled \(\Lambda\). (This rescaling is necessary as the Chebyshev polynomial form orthonormal basis in the interval [-1,1] and the eigenvalues of original Laplacian \(\Lambda\) lies in the interval [0,\(\lambda_n\)]).

Hence, the spectral convolution for graph with parametrized filters is given by:

\(y_i = \sum_{k=0}^{K}g_{\Theta_{k}}(\tilde{\Delta}) x_{i,k}\)

where, \(x_{i,k}\) are the input feature maps, \(\Theta_{k}\) are the trainable parameters.

Pooling Operation on graphs:

In case of images, the pooling operation consists of taking a fixed size patch of pixels, say \(2\)x\(2\), and keeping only the pixel with max value (assuming you apply max pooling) and discarding the other pixels from the patch. Similar concept of pooling can be applied to graphs.

The pooling operation on graphs consists of grouping the similar nodes and keeping only the few of the nodes from each group, instead of keeping all nodes in graph. Doing this multiple times is equivalent to multi-scale clustering while maintaining the local geometric structure. The pooling operation is also called as graph coarsening, as you get coarser (abstract level) graph after pooling.

The authors use coarsening step of Graclus multilevel clustering algorithm. It uses greedy algorithm to build coarser versions of graph.

Experiments:

To verify the effectiveness of the proposed convolutional neural network, the authors test the model on the Euclidean domain data. They have used MNIST dataset where each image is represented as graph and task is to classify these images. The network with two layers of proposed graph convolution layer was used for the experiment. The results were compared against the LeNet-like network with 2 CNNs. The accuracy obtained by proposed algorithm was 99.14 which is comparable with the one obtained by LeNet i.e. 99.33.

The second experiment was done on 20NEWS dataset. Each document was represented as graph and the goal here is to classify documents. The results were compared against linear SVM, multinomial Naive Bayes and fully connected network. The proposed spectral graph convolutional network was able to outperform fully connected network, which uses many parameter.

Conclusion:

• The non-Euclidean data such as graphs creates some challenges in applying the traditional convolution operation directly on the graphs. 
• However, by using the Convolution Theorem, which says convolution operation in spatial domain is equivalent to element-wise multiplication in Fourier domain. Hence, the convolution for graphs is defined in Fourier domain.
• The graph Fourier transform is calculated by multiplying the signal with the Fourier basis matrix.
• Learning spectral filters by performing convolution in Fourier domain has few limitations. Defferrard et al. address these issues by defining filter as a truncated Chebyshev polynomial of order \(K\).
• The proposed graph convolution network has the \(O(n)\) computational complexity. 

More Links:
- Paper Summary #1: Learning Convolutional Neural Networks for graphs(ICML 2016) 
- Notes on Deep Geometric Matrix Completion for Recommendation Systems
- Summary of talk on Overview of Convolutional Neural Network for Graphs at workshop on New Deep Learning Techniques, IPAM UCLA